|
Perhaps a more appropriate title for this page might be ‘Operating Considerations for LM355 Temperature Sensors from 3.3 Volt Supply using a Discrete Temperature-Compensated Constant Current Source’, but this is a little unwieldy and won’t fit nicely in the title block.
The Background
A friend is building a greenhouse environment controller. The temperature sensors that he has settled on are LM335 three terminal integrated circuits in a TO92 package. These are relatively low cost integrated circuits in a small TO92 package that work over -40 to 100°C, with a typical design current of 1 mA per device. They are readily calibrated to within +/- 2°C using a single 10 K Ohm trim pot.
LM355’s are readily insulated and hermetically sealed. The National Semiconductor Data Sheet recommends using heat shrink, but my preferred method is to use a plastic tube potted with either wax or epoxy.
Optimum greenhouse temperature is around 27°C, but we can expect the temperature to vary with location (soil and near the roof apex) and season. Let’s assume a maximum temperature of about 40°C which would be devastating for most vegetation, except perhaps cacti and other arid region flora.
For this application the available supply voltage is regulated 3.3 V. Supply voltage regulation is critical to this design, otherwise we have the added challenge of establishing a temperature stable voltage reference which is challenging using discrete components (integrated band-gap techniques come to mind).
A 3.3 V supply doesn’t give much headroom for an LM335 with an output voltage of 10 mV/K. In the most basic configuration an LM335 requires just a simple resistor, but with a 3.3 V supply this leads to a relatively large variation in operating current (exceeding device limits), changing the dynamic impedance and causing a variation in self-heating.
A better approach, which is also more appropriate for long sensor cables, is to drive the LM335 from a constant current source. A constant current source also eliminates LM355 output voltage variation due to changes in operating current.
For this application there are a number of temperature sensors so we need a number of constant current sources. Or do we?
Before I get too carried away, it’s worth while considering integrated circuit solutions. The cost of an integrated circuit constant current source such as an LM334 is almost twice that of an LM335 temperature sensor, needs an additional programming resistor, the programmed current is not temperature invariant, and the 0.9 V minimum operating voltage means they cannot be used directly with an LM335 from a 3.3 V supply.
We can make discrete MOSFET or JFET current sources with just one additional resistor but they require manual adjustment because of the wide variation in device parameters, there is no temperature compensation, and the forward voltage drop is still going to be a challenge for this application with a 3.3 V supply.
A Discrete BJT Design
So let’s steal some bipolar integrated circuit tricks and apply them to make a discrete temperature-compensated constant current source (or sink) design with a very low forward voltage drop and predictable performance.
Silicon Bipolar Junction Transistors (BJTs) are as cheap as – wel chips. In sensible qualities general purpose small signal transistors are less than $0.05 each. And perhaps with the exception of DC current gain, their parameters are remarkably predictable for a given device.
The reference for this design is Sedra, S. and Smith K. C., Microelectronic Circuits, Holt-Sauders Int. Ed., 1982, pp 430 et seq. While the text gives the design equations, derivation is left as an exercise (but I have included it below). This was one of my electrical and electronic engineering texts from university days and although I have studied it (it isn’t a casual read) from cover-to-cover I still refer to it from time to time. The stuff that is hidden books never ceases to amaze me.
Here is the basic circuit. It provides three first-order temperature compensated current sources with a minimum forward voltage drop of about 0.1 V (subject to the transistors and the current). The component cost for a discrete through hole design about $0.40 and half this for SMD devices.
Note that I have not used complimentary NPN and PNP transistors because there is no need provided that Q1 to Q3 and Q4 to Q7 are of the same type. Pretty much any general purpose small signal BJT’s should work.
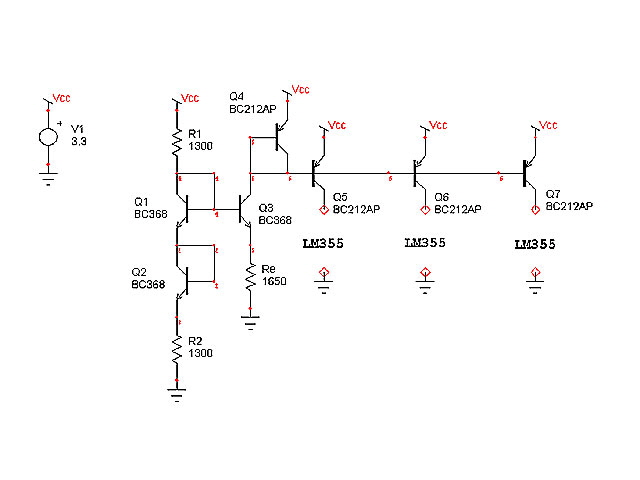
Figure 1. Discrete Temperature Compensated Constant Current Source
Note that Q1 to Q3 and R1, R2 and Re should be closely thermally coupled. This is readily achieved by keeping the components close together and away from any other components that are expected to get hot.
You can simply copy this design for your own applications that require one or more temperature-compensated 1 mA constant current sources. You can adjust the resistor values to provide other current values (within the limits of the transistor ratings). And you can invert the circuit (replacing NPN for PNP) to provide constant current sinks.
The two design equations are:
But for those folk that want to understand how this circuit works you might like to read on.
Analysis
Transistors Q1, Q3 and Q4 are connected as diodes to form a Vbe voltage reference. But they are still acting as transistors in the active mode in this configuration because Vcb = 0.
Q1, Q2 and Q3 and the three associated resistors R1, R2 and Re form the temperature compensated constant current sink with the collector of Q3 being the current sink.
Q4 through Q7 form a current mirror. The current sources are the collectors of Q5, Q6 and Q7. Additional transistors can be added in a similar manner, although eventually the cumulative base currents will become an issue.
Let’s start our analysis by assuming that the base emitter voltage, Vbe, in Q1, Q2 and Q3 are equal. The condition for this is that the collector current, Ic, and the temperatures equal because the forward voltage drop across a forward biased silicon junction is approximated by:
The constant n and Is (the saturation current which has temperature dependence) are often specified in the device data sheet or can be measured. n is typically in the range 1 to 2 and Is is likely to be of order 1E-16 Amps for a small signal device at standard temperature.
The voltage at the base of Q1 and Q3, can be estimated by neglecting the base currents (which are typically <100th of the collector current at DC). Applying Kirchhoff's Voltage Law (KVL) by inspection:
For Q3:
And for Q1:
If we equate [5] and [6] we have:
Rearranging to solve for Ic:
Expanding and collect terms in Vbe:
In this form you can see the influence of the temperature dependant Vbe term on the collector current, Ic. Now if we make R1 = R2 then 1 - 2 R2 / (R1 + R2) = 0 and the collector current is independent of Vbe and therefore temperature (at least to first order)!
Substituting R1 = R2 and simplifying:
The final part of the analysis is to ensure that the collector current in Q3 is equal to the collector currents in Q1 and Q2 (one of our two our initial assumptions). Neglecting base currents we can write expressions for the collector currents in Q1, Q2 and Q3 using Kirchhoff's Voltage Law (KVL) by inspection.
Q1 and Q2:
Q3 collector current is the Q3 emitter voltage divided by Re:
Equating [11] and [12] and solving for R1 (because Re is determined prior to R1 in order to establish the constant current):
(Vcc – 2 Vbe) / (2 R1) = Vcc / (2 Re) [13]
2 R1 = 2 Re (Vcc – 2 Vbe) / Vcc
R1 = R2 = Re (1 – 2 Vbe / Vcc) which is [2]
We can expect that for modest collector currents Vbe will be about 0.7 V at room temperature from [3]. This is a commonly used approximation of Vbe for silicon transistors in active mode at room temperature.
So to design our circuit we select Re for the desired constant current Ic and the available supply voltage Vcc. Solving [12] for Re:
And using [2]:
Now let’s think about the current mirror Q4 to Q7.
If we neglect base current as previously justified then Q4 has the same collector current as Q3 and is in the active mode. And the Q4 base emitter voltage Vbe is established by the Q3 collector current. If we connect the base of Q4 to the bases of Q5, Q6, Q7 then the collector current in each of these transistors will also be equal to the Q3 collector current.
But Q5, 6 and 7 are not diode-connected which means that if the collector current in any of these devices is below the Q3 collector current they will be driven into saturation, Vce will approach Vce(sat), the saturation voltage of the transistor, and Vbe will rise due to Ohmic losses causing a slight reduction in the collector current.
At modest currents up to say 1 mA, Vce(sat) is typically 0.1 V for small signal silicon transistors. This should enable an LM335 to operate from a 3.3 V supply up to a temperature of at least 45°C. Note that special transistors are available with very low Vce(sat) but these devices are not $0.05 each.
We could also implement a current mirror using MOSFETs or JFETs which overcomes the problem of
Vce(sat), but the turn on voltage in a FET, Vgs(on) is not a well defined device parameter. So FETs would need to be matched for Vgs(on).
Performance
Short of actually making the circuit we can test the performance using a SPICE simulation using ICAP. With the component values in the schematic at Figure 1, the simulated Q5 to Q7 source current is shown in Figure 2 from 0 to to 50°C.
The current slope is 120 nA/°C or over the 50°C temperature range which is essentially constant.
Now let’s consider what happens to the source current as Q5 to Q7 go into saturation with the circuit operating at 27°C (our greenhouse ideal temperature). This test checks out what happens with an LM335 operating at elevated temperatures. I’ve simulated an LM335 as a voltage source of 10 mV/K in series with an 0.5 Ohm resistor.
As expected the constant current curve starts to drop off above 40°C due the Vce(sat) and the 3.3 V supply, but an LM355 should still operate from this constant current source up to 55°C. This is significantly better performance than operating an LM355 with a 330 Ohm resistor (which provides a current of 1 mA at 24°C ) because the LM355 operating current varies significantly with sensed temperature, and falls below the 0.4 mA lower bound at an upper of temperature of about 44°C.
You can see from Figure 3 that if reduce the LM355 operating current to say 0.6 mA then we can extend the constant current region to almost 55°C, but read the data sheet carefully before making this change as it will affect calibration. This is similar to reducing amplifier gain to increase bandwidth, a story for another time.
|